- CEMC Home
- About Us
- Contests
- Courseware
- CEMC Digital
- CEMC in Person
- Books
- Master of Mathematics
for Teachers - Educator Development
- Make a Difference
- Frequently Asked
Questions
Demystifying Solar Eclipses through Math
By Paul McGrath
On April 8, 2024, the Moon's shadow will sweep across a relatively narrow strip of the Earth's surface. To be in the right place at the right time for such an event, a solar eclipse, is quite rare. Here in Waterloo, Ontario, we will be treated to a partial eclipse of the Sun during this event. However, one does not need to travel far from Waterloo (e.g., Niagara Falls) to get into the path of totality to observe a total solar eclipse. In the path of totality, the Moon will - if only for a few minutes - completely block out the Sun making it possible to observe the Sun's magnificent corona.
I stated above that it is rare to observe a solar eclipse and it is even more so to observe a total solar eclipse, but why is this? After all, a solar eclipse occurs when the Moon passes between the Sun and the Earth, so shouldn't this happen once every time the Moon orbits the Earth when we have a new moon? It's not quite this simple because the plane in which the Moon orbits the Earth is inclined relative to the plane in which the Earth orbits the Sun by about \(5°\). This means there is only an approximately 35-day interval, roughly every six months, during which eclipses can occur. We call these intervals eclipse seasons. This does, however, mean that there are two to three eclipses (including lunar eclipses) happening every eclipse season!
So, if solar eclipses are taking place at least a couple of times per year, then what makes observing a solar eclipse so rare? This has more to do with the size and nature of the shadow swept out by the Moon. Consider the following diagram illustrating the Sun illuminating space around the Moon.
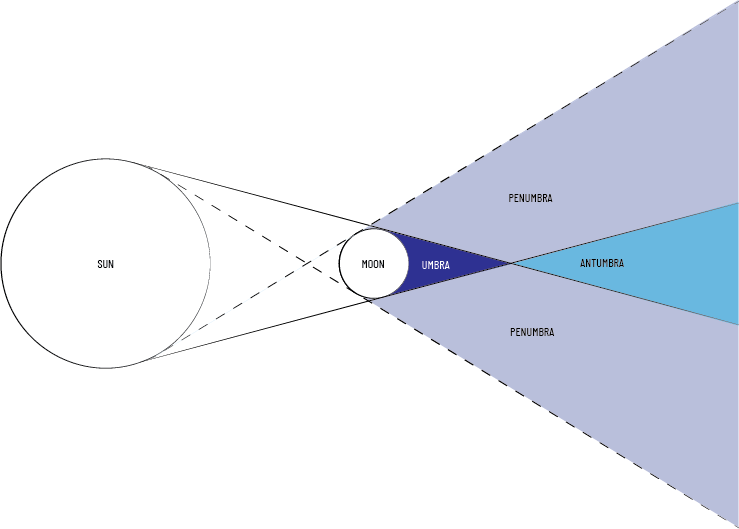
Since the Sun is not a point source of light, we can identify the region of space from which the Moon will completely block out the Sun by following the light rays emitted from the surface of the Sun along a path tangent to and on the same side of both the Sun and the Moon. In the two-dimensional representation above, there are two such lines but in three-dimensions, these rays enclose a conical region. The part of that region between the Moon and the vertex of the cone is called the umbra and this is where you must be to observe a total eclipse.
Let's note two other regions of interest. First, if you are in the conical region on the other side of the vertex which we call the antumbra, then you'll be able to see the rays of light tangent to the Sun and the Moon. However, you still have the Moon between you and some portion of the Sun. This means you're in a region where you'd observe an annular (ring-shaped) eclipse. Second, notice that there is a region which we call the penumbra in which the Sun will be partially obscured including some part of its edge. In this region, you'll observe a partial eclipse.



Figure 1: Left: A total eclipse as seen from within the Moon's umbra. Middle: An annular eclipse as seen from with the Moon's antumbra. Right: A partial eclipse as seen from within the Moon's penumbra.
During a solar eclipse, the Earth passes through the penumbra. Depending on where the Moon is in its orbital plane, the Earth may also pass through the umbra or antumbra. Which of these it passes through further depends on the Earth-Moon orbital separation which varies between \(356 \, 400\) km and \(406 \, 700\) km. Using a bit of geometry, let's roughly work out at what orbital separation distances we could expect to observe total versus annular solar eclipses. This is an approximation because I'll assume for simplicity that the shadow is a circular disk centred just in front of the Earth with the Earth, Sun, and Moon in perfect alignment.
Let \(r_{S}\) be the radius of the Sun, \(r_{M}\) be the radius of the Moon, \(r_{E}\) be the radius of the Earth, \(d_{ES}\) be the Earth-Sun orbital separation distance, \(d_{EM}\) be the Earth-Moon orbital separation distance, \(r_{u}\) be the radius of the umbral shadow, and \(x\) be the distance from the centre of the Earth to the vertex where the umbra meets the antumbra.
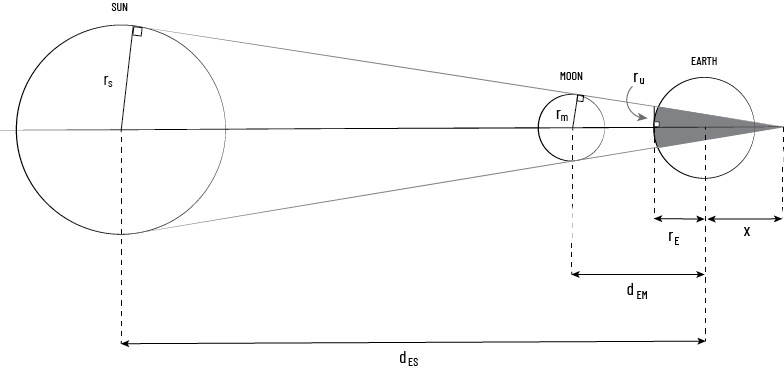
Using similar triangles and assuming\(^{1}\) \(d_{ES}\) is much greater than \(x\), we can argue that
\(\frac{r_S}{d_{ES}} = \frac{r_M}{d_{EM}+x}=\frac{r_u}{r_E + x}\)
After some algebraic manipulation, we can eliminate the quantity \(x\) and show
\(r_u = r_M - \frac{r_S}{d_{ES}}\left(d_{EM} - r_E\right)\)
For the April 8 eclipse, the Earth-Moon orbital separation \(d_{EM}\) will be approximately \(359 \, 500\) km. The other values on the right-hand side are approximately given by \(r_S = 696 \, 000\) km, \(r_M = 1 \, 740\) km, \(r_E = 6 \, 380\) km, and \(d_{ES} = 150 \, 000 \, 000\) km. With these values we find \(r_u \approx 102\) km.
If we were trying to determine more precisely the size of the Moon's shadow as it sweeps across the surface of the Earth, then some further adjustments could be made which would basically amount to projecting the disk whose radius we just found onto the surface of a sphere. However, the value of \(100\) km gives us a good starting point and also helps answer the question of why observing a solar eclipse is so rare. Compared to the full surface area of the Earth, the path swept out by a shadow this size is quite small.
The final piece of the puzzle explaining why total solar eclipses are so rarely seen from any one spot on Earth has to do with the variation in the Earth-Moon separation distance. Observe that the April 8 value of \(d_{EM}\) we used (\(359 \, 000\) km) is quite close to the minimum Earth-Moon separation distance (\(356 \, 400\) km). The smaller \(d_{EM}\) is, the larger the Moon's shadow on the Earth will be. For example, if the distance were just \(10 \, 000\) km greater, then the umbral shadow radius would drop to approximately \(55\) km. Moreover, for distances between roughly \(381 \, 400\) up to the maximum separation distance of \(406 \, 700\), the surface of the Earth sits in the antumbra region and an annular eclipse would be seen instead of a total eclipse.
Given how rare it is to observe a solar eclipses, how were early astronomers (possibly as early as 585 BC) able to predict the occurrences of eclipses? The reason is that the motions of the objects involved are all periodic. This means that the conditions required for an eclipse to occur repeat with a certain regularity and we can calculate how often this repetition happens by first identifying the periods for the three things needed for our Sun-Earth-Moon system to return to a previous state.
- The synodic month (29.530589 days) is the time it takes for the Moon to orbit the Earth once with respect to a line passing through the Earth and the Sun. (The Moon will go through all of its phases in one synodic month.)
- Since the Moon's orbit is inclined relative to the Earth-Sun plane, its position fluctuates above and below this plane but it must be in this plane for an eclipse to occur. The draconic month (27.212220 days) measures the length of this cycle.
- The Moon's orbit is elliptical and precesses slowly (i.e., the orientation of the ellipse rotates over time like a drawing on a Spirograph). The anomalistic month (27.554551 days) measures how long it takes for the Moon to complete one cycle of this precessing path.
It turns out 223 synodic months, 242 draconic months, and 239 anomalistic months are all nearly equal to 18 years, 10 - 12 days (depending on number of leap years in between), and 8 hours. We call this length of time a saros. This means that we can expect another total solar eclipse one saros later, on April 20, 2042. The only catch is that the extra 8 hours means the path of the eclipse will land about 120° west of where it will in 2024. This is easy enough to account for however and explains how future eclipse events can be predicted based on previous eclipse observations. Of course, nowadays, we use computers to very carefully forecast the dynamics of the Sun-Earth-Moon system and generate highly accurate predictions.
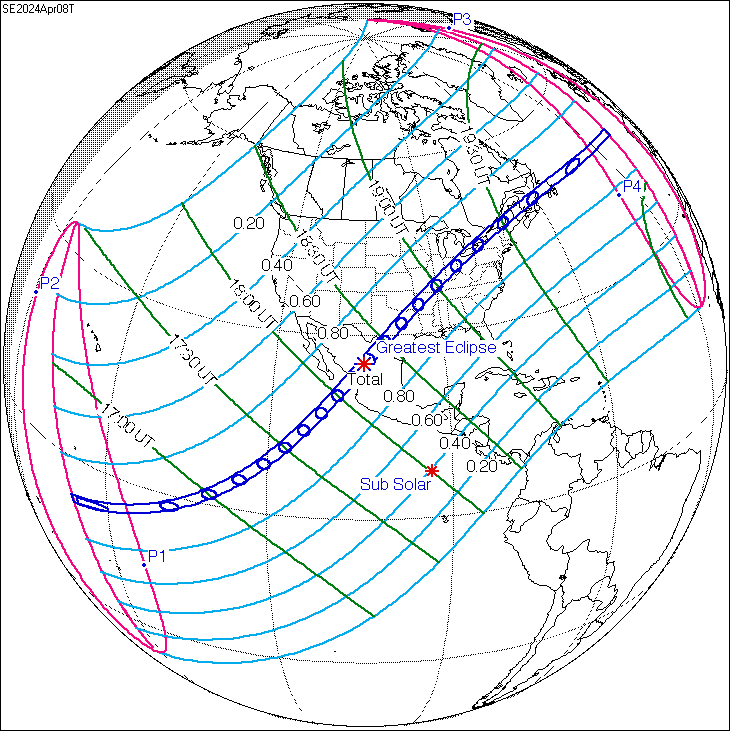
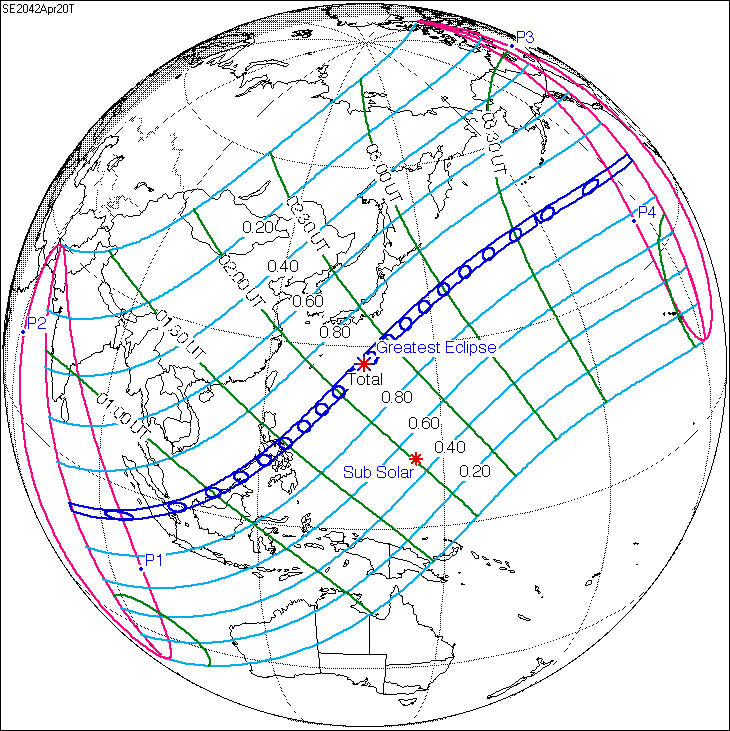
Figure 2: The April 8, 2024 solar eclipse path (left) compared to the April 20, 2042 solar eclipse path (right) which will occur one saros later.
I hope that you will have the opportunity to view the April 8 solar eclipse or another one closer to you in the future. I just want to leave you with one final note on safety. Aside from the short time in which the Sun is completely eclipsed, be sure to only observe the Sun with proper eye protection. Sunglasses do not cut it. You'll need solar eclipse glasses or something similar which has been manufactured specifically for this purpose and complies with the ISO 12312-2 international standard safety requirements. With those on hand, you'll be ready to enjoy this spectacular event!
\(^{1}\)The value of \(x\) varies by approximately \(50 \, 000\) km while \(d_{ES}\) is approximately equal to \(150 \, 000 \, 000\) km and itself varies by about \(5 \, 000 \, 000\) km, so this is a very safe approximation.
Images Used:
Total Eclipse
Annular Eclipse
Partial Eclipse
April 2024 Eclipse
April 2042 Eclipse



 CEMC
CEMC